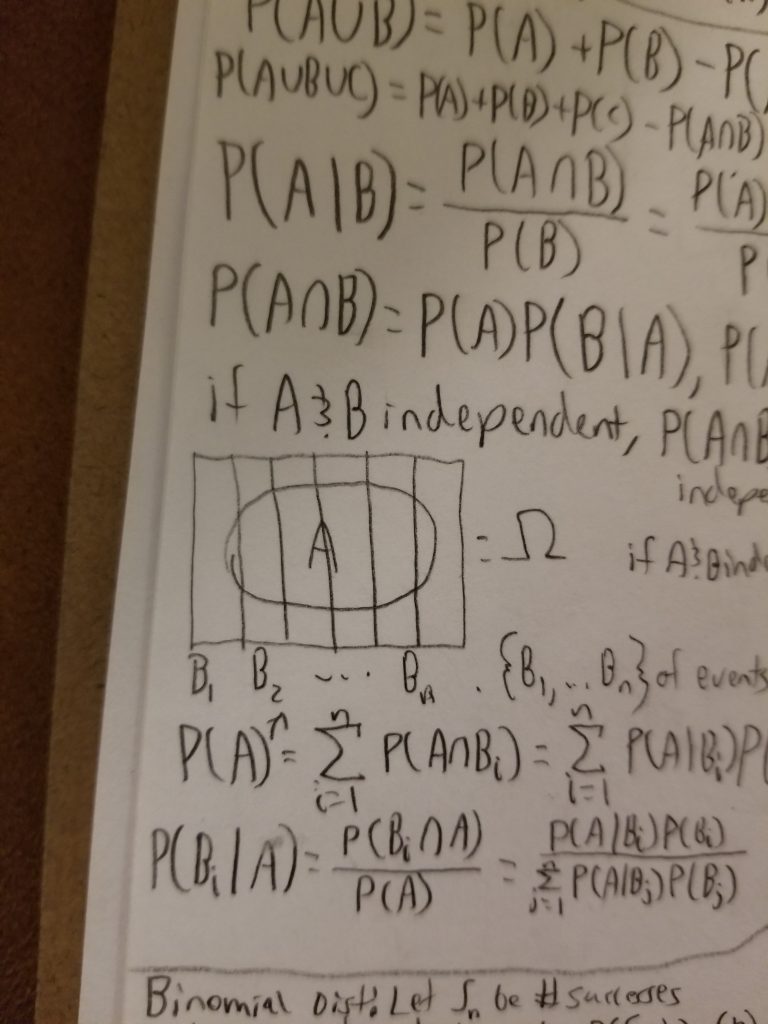In the United States constitution, it is stated that “We the People of the United States, in Order to form a more perfect Union […] establish this Constitution for the United States of America.” What type of union is more perfect than the union of partitions of disjoint events?

Here I will compare the definition of a partition with the Union of states as discussed in the Constitution. The definition of a partition is as follows: a partition of a set X is a set of non-empty subsets of X such that every element x in X is in exactly one of these subsets (i.e., X is a disjoint union of the subsets). We see this idea that the Union of States (the United States) is a partition, shown in the Constitution in Article IV, section 3 on the discussion of the formation of new states. There it says that new states can be admitted into congress, but it cannot be formed or erected in the jurisdiction of any other state unless through agreement, and in section 4 it states that every state in the Union is guaranteed a republican form of government. As shown here, we can conclude that the United States is indeed a partition of the states it makes up: since each state is disjoint, and that the intersection of the states are the null set (no states share jurisdiction), and the union of all the states makes up the United States, then each state is thus a partition. In relation to the picture below, Ω represents the United States, where each subset Ω B1, B2, …, BN represents each state (a partition of Ω).

It is true however that the states are subordinate to the national government though. Could you disprove the notion that states are partitions of the United States by disproving the statement that the states are disjoint?